Regression Analysis - Part 1
In this post, I will mainly deal with Simple Linear Regression on the Advertisement dataset.
The dataset contains 4 features:
Yes, there is a relationship between advertising budget and sales. From the plot, TV has the best relationship.
Question 2: " How strong is the relationship between advertising budget and sales? "
TV and Sales has a strong relationship with a correlation factor of 0.78, whereas Radio and newspaper has poor relationships with correlation factor of 0.57 and 0.22 respectively.
Residual Standard Error = 3.26 [can be calculated by taking square-root of mse-resid]
Best Fit Line : Sales = 7.0326 + (0.0475 * TV)
Things to note:
For this, we will use the Bartlett's test.
Null Hypothesis : the variance is constant
Alternate hypothesis : the variance is not constant
Results: Statistic: 10.195
p-value : 0.001
So, with p-value < 0.05, we reject the null hypothesis and conclude that the constant variance assumption does not hold.
Lets do some transformations on the variables.
log transformation - Power Model has the best results.
1. R2 score : 74.2%
2. Residual Standard Error: 0.211
3. Durbin-Watson : 1.98, i.e. positive auto-correlation, which is good.
4. Condition no : 23.7, i.e. there is no multicollinearity, since it is very less.
5. AIC : -52.91
BIC : -46.31, both explains the goodness of fit, lower the better.
6. F-statistic : 569.8
P-value : 3.51e-60
More than 95% of the standardized residuals should fall under -2 and +2. Then, we cannot question the assumption that error term has a normal distribution.
Looking at the plot, we can see a couple of points outside -2.
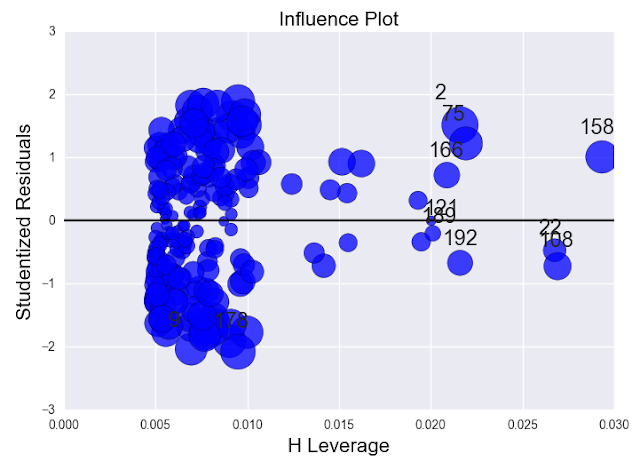
Lets look at the influence plot to confirm this.
Leverage plot catches those outliers which the standardized residuals plot couldn't. In this case, observation number 9 and 178 are beyond the range -2. But point 9 has a less leverage value whereas 178 has a slightly higher leverage value.
Now, points 158, 108 and 22 have high leverage value but low residual. So they can't be marked as outliers. Although they can be marked as high leveraged points.
Lets create 3 more models:
Model 1: delete high residual points 9 and 178 and check our model.
Model 2: delete high leveraged points 158,108 and 22.
Model 3: delete all the above points.
Results:
Model 1 gave the best results.
1. R2 score : 75.3%
2. Residual Standard Error: 0.207
New Best Fit Line ----------> log(Sales) = 0.8936 + (0.3585 * log(TV))
Also, there is a massive reduction in Residual standard error from 23% to 1.4%
The dataset contains 4 features:
- TV : Amount of expenditure on TV advertisements
- Radio : Amount of expenditure on Radio advertisements
- Newspaper : Amount of expenditure on Newspaper advertisements
- Sales : Amount of sales occured
Section 1:
Question 1: " Is there a relationship between advertising budget and sales? "Yes, there is a relationship between advertising budget and sales. From the plot, TV has the best relationship.
Question 2: " How strong is the relationship between advertising budget and sales? "
Section 2:
In this section, we will deal with our regression analysis with just 1 predictor. TV expenditures will be considered, since it has the best relationship with sales.Residual Standard Error = 3.26 [can be calculated by taking square-root of mse-resid]
Best Fit Line : Sales = 7.0326 + (0.0475 * TV)
Things to note:
- only 61% of variability in sales can be explained by TV expenditures.
- with p-value < 0.05, TV is statistically significant.
- coefficient = 0.0475, i.e. for an increase in $1000 in TV expenditure, sales will increase by 48 units.
- Since, RSE = 3.26, i.e. actual sales in each market deviate from the true regression line by approximately 3,260 units, on average.Mean Sales across all markets: 14000 dollars
Percentage of error: 3260/ 14000 = 23%, i.e. our model has an error rate of 23%.
Assumptions Check:
- Linearity : hold
- Constant Variance : does not hold, i.e. funnel shaped residuals
- Normality : hold
- Independence : hold
For this, we will use the Bartlett's test.
Null Hypothesis : the variance is constant
Alternate hypothesis : the variance is not constant
Results: Statistic: 10.195
p-value : 0.001
So, with p-value < 0.05, we reject the null hypothesis and conclude that the constant variance assumption does not hold.
Lets do some transformations on the variables.
Section 3:
Transformations methods to be used:
Results:
log transformation - Power Model has the best results.
1. R2 score : 74.2%
2. Residual Standard Error: 0.211
3. Durbin-Watson : 1.98, i.e. positive auto-correlation, which is good.
4. Condition no : 23.7, i.e. there is no multicollinearity, since it is very less.
5. AIC : -52.91
BIC : -46.31, both explains the goodness of fit, lower the better.
6. F-statistic : 569.8
P-value : 3.51e-60
Section 4:
Residual Analysis:
More than 95% of the standardized residuals should fall under -2 and +2. Then, we cannot question the assumption that error term has a normal distribution.
Looking at the plot, we can see a couple of points outside -2.
Lets look at the influence plot to confirm this.
Leverage plot catches those outliers which the standardized residuals plot couldn't. In this case, observation number 9 and 178 are beyond the range -2. But point 9 has a less leverage value whereas 178 has a slightly higher leverage value.
Now, points 158, 108 and 22 have high leverage value but low residual. So they can't be marked as outliers. Although they can be marked as high leveraged points.
Lets create 3 more models:
Model 1: delete high residual points 9 and 178 and check our model.
Model 2: delete high leveraged points 158,108 and 22.
Model 3: delete all the above points.
Results:
Model 1 gave the best results.
1. R2 score : 75.3%
2. Residual Standard Error: 0.207
New Best Fit Line ----------> log(Sales) = 0.8936 + (0.3585 * log(TV))
Conclusion:
Comparing our final model to the baseline model we see that, R2 score increased significantly from 61.2% to 75.3%.Also, there is a massive reduction in Residual standard error from 23% to 1.4%












Comments
Post a Comment