Artificial Neural Network Project 1– Churn Modelling

Aim:

The main purpose of this post is to show how KerasClassifier(), i.e. an Artificial Neural Network can be used to predict a target variable. And how we can tune the parameters of a Neural Network to obtain a better model.

Dataset: 

For this purpose, I have used the Churn Modelling dataset, in which the model has to predict whether the customer will leave the bank or not.

Initially, I will build 7 models with different network structures and select the best model for further tuning.

Common parameters for each model:

1.   Epochs       = 150

2.   Batch_size = 10

3.   Optimizer  =  adam

4.   Activation function  = relu

5.   Network Weight Initialization = uniform

The dataset was divided into 75% training set and 25% validation set.

Models used:

Model 1:  Sequencial Model: a sequential model is a linear stack of layers.

               Network Structure:  [6 --> 1]

	Accuracy	Loss
Training	0.85	0.37
Validation	0.85	0.38

Model 2:  Base KerasClassifier: Network Structure:  [6 --> 1]

	Accuracy	Loss
Training	0.86	0.35
Validation	0.85	0.35

Model 3:  KerasClassifier Small Model: Network Structure:  [3 --> 1]

	Accuracy	Loss
Training	0.83	0.40
Validation	0.84	0.41

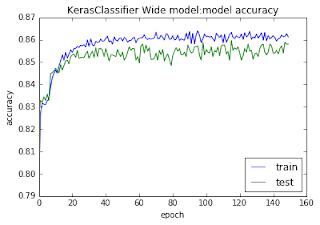
Model 4:  KerasClassifier Wide Model:  Network Structure:  [12 --> 1]

	Accuracy	Loss
Training	0.86	0.35
Validation	0.85	0.36

Model 5:  KerasClassifier Large Model:  Network Structure:  [6 --> 3 --> 1]

	Accuracy	Loss
Training	0.79	0.51
Validation	0.80	0.50

Model 6:  KerasClassifier Deep Model: Network Structure:  [6 --> 3 --> 2 --> 1]

	Accuracy	Loss
Training	0.79	0.51
Loss	0.80	0.50

Model 7:  KerasClassifier Wide and Deep Model:

               Network Structure:  [12 --> 6 --> 3 --> 1]

	Accuracy	Loss
Training	0.84	0.40
Validation	0.83	0.41

Best Models:

From the mean accuracy scores and model loss, 2 models have performed better than others. They are Model 2 and Model 4, i.e. [Base KerasClassifier and Wide Model].

Lets look at some prediction diagnostics of these two models.

Looking at the recall’s, Model 4 performs better in predicting the type 1 class, about 52% as compared to 38% in Model 2.

Also the overall precision, recall and f1-score are better for Model 4.

Lets tune Model 4 to obtain a better model:

	Parameters	Best parameter	Best Score
Epochs and Batch_size	Epochs: [50, 100, 150] Batch_size : [10, 20, 40, 60, 80, 100]	Epochs  =  50 Batch_size =  60	85.93
Optimizer	['SGD','Adam','RMSprop','Adagrad', 'Adadelta', 'Adamax', 'Nadam']	Nadam	85.74
LearningRate	[0.001, 0.01, 0.1, 0.2, 0.3]	0.01	85.70
Network Weight Initialization	['uniform', 'lecun_uniform', 'normal', 'zero', 'glorot_normal', 'glorot_uniform', 'he_normal', 'he_uniform']	Glorot_normal	85.96
Neuron Activation Function	['softmax', 'softplus', 'softsign', 'relu', 'tanh', 'sigmoid', 'hard_sigmoid', 'linear']	Relu	85.84
Dropout and weight_constant	weight_constraint = [1, 2, 3, 4, 5] dropout_rate = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6]	Dropout = 0.6 Wt_constant= 4	86.05
No. of Neurons	[1, 5, 10, 15, 20, 25, 30, 40]	40	85.70

Final Model:

Although the overall precision, recall and f1-score of the tuned model remained same as the base model, if you look at the model accuracy and model loss graph of the final model, we notice that the model performs better in predicting the testing data, even better than training.

We are able to predict 45% of the people who are going to leave correctly and 97% of the people who will stay, an overall recall of 86%.

To view the full code for this project on Github, Click Here